00:00:11.120
Hello RubyConf! My name is Tom, and I'm a senior staff engineer at Shopify. Today, I'm here to talk to you about programming.
00:00:17.760
Almost exactly ten years ago, at the end of October 2011, I gave a talk called "Programming with Nothing" at the Ruby Manor conference in London. Although the details of that talk aren't crucial, I'll briefly summarize its conclusion to build on it today.
00:00:25.439
In that talk, I demonstrated that it is possible to write useful programs in Ruby using only procs. This is because we can encode any data structure with procs and implement operations on those encoded data structures.
00:00:36.480
For example, one way to encode a number as a proc is to call it once with a function p, then again with an argument x, allowing p to be called on x a fixed number of times.
00:00:49.920
So, the encoding of the number three would call p three times. If you're not familiar with the pointy arrow and square brackets syntax, it's simply a more concise way of writing a lambda and call, and I'm using it here to keep the code compact.
00:01:02.640
Not surprisingly, this encoding lets us represent numbers as large as we like, such as five, fifteen, or one hundred. These encodings are legitimate because we can convert them back into Ruby numbers whenever necessary. For instance, if we take the Ruby proc that adds one to its argument and call it on the Ruby zero object three times, we get the Ruby three object. Similarly, this also works for one hundred, and if we call it zero times, we simply get the original Ruby zero object back.
00:01:28.080
The encodings of numbers are not only legitimate, but they are also usable for computation. We can implement operations like increment, decrement, addition, and subtraction in the same way. These operations are a bit complex, so I won't delve into the specifics, but the important takeaway is that they work.
00:01:42.560
For example, I can add an encoded five and three together to yield an encoded eight and then check its Ruby value to confirm the computation. Similarly, I can raise an encoded two to the power of an encoded eight, and when I decode it, I get the Ruby number 256 as expected.
00:02:10.319
We can encode even more complex data structures like pairs and lists, which include operations such as checking for the empty list, fetching the first list item, or obtaining the rest of the items. More complex operations can generate an encoded list of all encoded numbers within a certain range or map an arbitrary function over an encoded list.
00:02:28.879
This framework provides us everything we need to fully implement FizzBuzz, with all its data and operations encoded as procs. At the end of my "Programming with Nothing" talk, I showed that we can inline expand all these constants, which represent other procs, to achieve a complete FizzBuzz implementation that is syntactically just procs.
00:02:54.160
I can demonstrate that by pasting it into a terminal and using some helper methods to decode it into a Ruby array of Ruby strings. There you go! It does slow down a bit towards the end as the numbers get larger, but it takes about eighteen seconds to print them all.
00:03:20.720
So, ten years later, I'd like to explore this topic further. That talk demonstrated that an extremely minimal subset of Ruby is still a fully capable programming language. Essentially, we are leveraging almost all the computational power of Ruby while only relying on a tiny fraction of its features.
00:03:48.000
In this talk, I want us to better understand that fraction by implementing it ourselves from scratch. This involves posing three questions. Firstly, could we represent these encoded values ourselves without using procs and their built-in behavior to represent numbers, lists, and so forth? Could we design and implement our own objects to achieve this?
00:04:00.799
Secondly, if we create our own objects for encoding values, can we explicitly evaluate them and recreate the computational behavior we get for free with procs? Lastly, if we can successfully recreate that behavior and perform computations with our objects, can we decode the results back into useful information afterward?
00:04:25.919
If we can do all three, we would no longer rely on Ruby's built-in implementation of procs to bring our encodings to life. We could construct our own implementation that we understand and control, and I believe that would be pretty cool.
00:04:51.120
Let's start with the first question: can we represent these encoded values ourselves? Can we roll up our sleeves and create our own honest, hard-working, artisanal data structure to represent encoded values, instead of lounging around expecting Ruby to be accommodating enough to let us use as many procs as we desire?
00:05:05.120
Well, yes, I believe we can. Let's consider some arbitrary Ruby value encoded as procs—this was the encoding of the number three. There are really only three kinds of syntax appearing here. Firstly, there are some variables—four in total, named p and x. Secondly, there are three calls. Finally, there are two proc definitions, each with a parameter name and a body.
00:05:17.280
The outer definition has the parameter name p, whose body is another proc definition. The inner one has the parameter name x, which contains the three nested calls. Notice that the parameter name isn't a variable; it's a special syntax for proc definitions to specify the name of the parameter, much like how a method parameter creates a local variable.
00:05:49.920
This flexibility in wiring up connections provides procs with enough computational power to achieve the functionality I described in the previous talk. This simplicity is excellent news because if we want to represent an expression like this, we need only concern ourselves with representing variables, calls, and definitions.
00:06:10.080
Those are the only three structural features visible in any of these encoded values, even in a substantial one like FizzBuzz. You can think of this as a wiring diagram that connects parameters to variables intricately, achieving its computational behavior.
00:06:30.160
We can create our own representation using structs, defining classes for variables, calls, and definitions, each with relevant components. A variable will just have a name, a call will consist of a receiver and an argument, and a proc definition will have a parameter name and a body.
00:06:48.000
To make these structs easier to work with, we can implement an inspect method on each class, allowing their instances to be formatted nicely when we examine them. Now we can create a new variable with the name x, a new call using this variable as the receiver and argument, or a definition whose body contains that call.
00:07:05.680
They will superficially resemble the real thing since these inspect methods format them like Ruby source code. However, they're not real variables or procs; they're structures made from objects whose behavior we control. For instance, we could create a composite structure to represent the encoding of the number three.
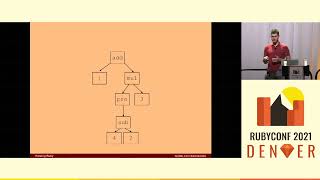
00:07:27.120
When we examine the structure of this representation, we see that it resembles a tree. There is a top-level definition including a parameter name, another definition containing yet another parameter name, and within it a call with further nested calls and variables. This kind of structure is known as an abstract syntax tree.
00:07:48.400
Thus, this is the abstract syntax tree of the proc encoding of the number three.
00:08:04.480
Representing these encoded values as trees is not overly complicated. However, if we already possess one of these encoded values as a Ruby proc in memory—like three or FizzBuzz—how can we convert it into our abstract syntax tree representation? I can conceive a few cumbersome methods to do this.
00:08:42.000
One approach is querying MRI for its YARV bytecode instructions, and then we might be able to analyze the proc's structure. Alternatively, we could utilize the disassemble method to generate a human-readable version and process that. If the proc was loaded from a file, we could also use its source location to find out which line it's on and read it in as a string, then apply Ripper from the standard library to parse that string into a structure we can evaluate.
00:09:01.360
However, I'm not keen on either of these options. The first is limited to MRI since YARV is MRI-specific, while the second relies on having the source code of the proc available as a file, which we might not if it was constructed at runtime.
00:09:23.760
Instead, I propose a third option, which involves using the behavior of a proc to reveal its inner structure. This way, we rely solely on the proc's functionality without making any assumptions about its origin or the Ruby internals.
00:09:40.000
For instance, we can query a proc like three about its parameters. This allows us to determine that it has one required parameter, named p. Pulling out the parameter name gives us half of the information we need, but how do we derive its body? We can think about a simpler case, like a proc called identity that returns its argument.
00:10:05.920
From the external perspective, we know that its parameter is called x, but we can't directly access its body. However, we understand that whatever argument we pass into the proc will replace all occurrences of x in its body. So, if we create a variable named x for that purpose and call the proc with that variable, we’ll simply receive the body back—in this case, the variable x.
00:10:21.520
This reveals that the proc's parameter is called x and its body is also the variable x. Now, let’s take another example, a proc called omega, which refers back to itself. We create a variable named the same as its parameter, but when we call that proc with our variable, an exception will occur because its body refers to the square brackets method on the variable we passed in.
00:10:37.520
This retrieves the struct square bracket method, looking up values based on a numeric index. To take advantage of this, we can redefine the square brackets method in the variable class to build a new call object, remembering the variable itself and the argument passed.
00:10:55.680
So, calling the proc again will yield a representation of its body. Finally, we can create a variable p and call the proc with it, receiving another proc back, which is the inner proc body.
00:11:17.440
This process gives us all the information necessary to reconstruct the original Ruby proc with our own representation. So, we need to wrap this technique into a method. Don’t worry about trying to decipher the code right now. It’s all available on GitHub if you’re interested, so just let it wash over you.
00:11:39.440
The main concept is to create a from_proc method that converts a proc into an expression. We accomplish this by creating a new variable object named after the proc's parameter, calling the proc with it as an argument. This way, every instance of the proc's parameter in its body is replaced by that variable object.
00:12:03.440
Next, we recursively convert the result in case the body of the proc is another proc, and we finally build a new definition object to return. We also need to replace the square brackets method on the variable, call, and proc classes to convert any receivers and arguments from procs using the method we just defined, wrapping the results in a call object.
00:12:27.120
I’ve chosen these three classes because they can all appear as the receiver inside a proc we’re converting. When we evaluate any proc body that contains a call, it will use this replacement method and create an instance of our call class without calling anything directly.
00:12:42.000
Note that in any production code, we would need to clean up these monkey patches later, as they might disrupt other code expecting the original methods. Now we can convert the proc encoding of three into our own representation. You can see it’s an instance of our definition class.
00:13:00.639
Likewise, for the proc encoding of FizzBuzz, there's our converted version, which is also a definition object.
00:13:14.880
Now that we have a representation of these proc encodings, we need to evaluate them ourselves so that we are not dependent on Ruby procs to execute computations, like adding two and three or FizzBuzz. This requires us to implement a method called evaluate that processes an abstract syntax tree.
00:13:29.600
However, it’s not obvious what that evaluation entails. A variable will refer to the parameter of some proc it is inside, potentially allowing us to retrieve an argument, while a call will have a receiver and an argument needing evaluation as well. For a definition, we will need to evaluate its body eventually, but not immediately—only when it is involved in a call elsewhere.
00:13:49.919
It sounds complex, and I’m not clever enough to solve this by myself, but fortunately, a mathematician called Alonzo Church wrote a paper in 1935 that outlines this process.
00:14:05.519
This paper addresses the same decision problem that Alan Turing took on by inventing Turing machines, and it's still incredibly insightful today, even being over eighty-five years old. For instance, it contains wonderful ideas about how to represent numbers as expressions resembling procs, the foundation of my previous talk.
00:14:24.480
So, thank you, Alonzo, for your contributions. The paper also discusses operations we can perform on these expressions; operation number two is called reduction, which refers to the process when you call a proc with an argument.
00:14:41.200
In Church's notation, the way to evaluate a call involves replacing all occurrences of the variable x in expression m with n. Here, x is the proc's parameter, m is the proc's body being called, and n is the argument used.
00:15:03.200
To examine this reduction idea with regular Ruby procs, let’s consider a proc p that takes a greeting and a name, returning an interpolated string. If I call it with the string 'Hello,' we get another proc back. However, the conceptual underpinning is that the argument 'Hello' has replaced the variable greeting in the body of p.
00:15:21.440
You might interpret the result as the body of p, but with one of its variables filled in with a value. If we then provide a second argument, the string 'RubyConf,' both variables are replaced with their corresponding values.
00:15:41.440
In Church’s paper, he explains that when we have numerous proc definitions and calls composed into a larger expression, each repeated reduction operation gets us closer to a fully evaluated result.
00:15:59.600
I will briefly show you how we can implement this operation on our abstract syntax tree representation. First, we need a helper method named replace, which takes a variable's name to replace, an expression to substitute, and an original expression for that replacement.
00:16:16.640
This method recursively traverses through the abstract syntax tree of the target expression. Whenever it finds a variable whose name matches the variable we’re replacing, it returns the replacement expression instead of the original variable.
00:16:34.240
An interesting situation arises when it encounters a definition whose parameter name collides with the name we’re replacing; in that case, it simply halts and returns the original definition. Since any variables with that name inside the definition's body must reference that parameter, we shouldn’t alter them.
00:16:51.760
As a side note, please be aware that a more complex implementation would be required if the replacement could contain variables whose names do not refer to any parameters. However, that’s not a concern in the cases we’ll be addressing.
00:17:06.720
Now, let's see how the replace method operates. Suppose we create three variables, a, b, and c, forming an expression that calls a with b and c as arguments. Using the replace operation, I can effectively swap out b for another expression, such as the identity proc we introduced earlier.
00:17:22.080
Alternatively, we might replace a or c instead, resulting in expressions where either variable has been substituted. Once we have the replace operation functioning, we can utilize it to reduce an expression by finding opportunities to pull out the definition body and substitute its variables.
00:17:40.000
To help with this, we’ll need another tool to ascertain whether an expression constitutes a value—a successful result of evaluation. Because we derive values by encoding procs, only proc definitions can count as values, while calls and variables cannot.
00:18:01.440
Moreover, we can implement Alonzo Church's reduction operation on expressions. In Ruby, since the evaluation strategy is left-to-right, we must navigate to the next part of the expression in the same sequence to replicate its behavior.
00:18:22.880
In general, we would reduce the left-hand side of a call, addressing the receiver first. If the receiver is already a fully reduced value, we would shift to reducing the right-hand side, which is the argument.
00:18:39.760
It's only in the specific scenario where the receiver is a definition and the argument is a value that we replace the parameter with the argument within the body of the receiver, as Church indicated.
00:18:55.680
To effectively evaluate an expression, we need to continually reduce it. For example, if I create expressions for adding one and two, followed by a call to add using one and two as arguments, I can keep reducing it.
00:19:11.840
If none of the patterns in the reduce method match, that indicates we can no longer reduce further, and thus the evaluation has concluded. As noted, we end with definitions at the top level, but since Church only explains how to reduce calls with variable replacement, it's logical we would stop here.
00:19:29.920
This can easily be wrapped in an evaluate method that calls the reduce method until none of its internal patterns match, allowing us to evaluate the entire expression in a single step.
00:19:49.760
Great! We have effectively represented and evaluated these values. Moving to the third problem: how do we decode the evaluation results to make sense of them?
00:20:05.760
You might have noticed that applying the addition of one and two yielded a result that looks different from what we previously identified as the encoded three, which is a bit problematic. These encoded values are only useful if we can revert them back into their Ruby equivalents.
00:20:22.160
However, if this abstract syntax tree doesn’t align with our conception of what three should appear as, how can we recognize it? To remedy this, we need to integrate the concept of a constant, which acts as an atomic value we can carry around, even without any behavior.
00:20:38.560
Constants will also be included in our abstract syntax trees, alongside variables, calls, and definitions. Constants feature names like variables but lack any inherent meaning, essentially serving as placeholders.
00:20:57.120
For constants to be useful, we must establish support for their evaluation. First, we need to enhance the value determination to include constants as recognized values, along with any calls where a constant is the receiver. Since constants lack behavior, we want them to remain inert in the face of function calls.
00:21:14.480
Now, if we take the outcome of adding one and two, followed by calling it with two defined constants—let's call them increment and zero, although the names are irrelevant—we observe that when evaluating this, we can interpret the results according to how many times the first constant appears.
00:21:32.400
If we invoke this conversion method on an encoded number, we receive the accurate Ruby integer back even if its structure is more complex than the simplest representation.
00:21:54.640
Thus, we have examined the capability to represent, evaluate, and decode these proc-encoded values ourselves rather than relying on Ruby’s proc implementation to complete the tasks.
00:22:11.200
This is a thrilling realization, and I believe it retroactively validates the challenges faced while programming with nothing initially. By confining ourselves to writing programs in this restricted Ruby subset, we have created opportunities to fully comprehend and implement that subset from scratch.
00:22:28.480
It feels empowering to have this level of insight and control over the underlying machinery in the process of computation, rather than just understanding the programs operating on top.
00:22:45.440
Here's a quick demo of converting the FizzBuzz proc into an abstract syntax tree and then interpreting that as an array of strings using our evaluate method.
00:23:02.400
As you can see, it works fine but there is a downside—it takes nearly two hours to print all the numbers up to one hundred, which is not practical.
00:23:19.840
Naturally, one might ask if we could speed things up. Our own approach requires two hours to execute FizzBuzz compared to approximately eighteen seconds for the native Ruby procs. While we can do the evaluations independently, improving performance would be advantageous.
00:23:43.520
Fortunately, in 1964, computer scientist Peter Landin published a paper titled "The Mechanical Evaluation of Expressions," which addresses this issue. This paper outlines a specification we now recognize as an abstract machine for evaluating expressions.
00:24:05.920
The machine's state consists of four data structures: stack, environment, control, and dump, leading to the nomenclature of the SECD machine. The control component is particularly crucial as it represents a command list waiting execution, while the stack contains intermediate evaluation results.
00:24:24.880
Each step of the machine updates its state according to the control commands that direct future actions.
00:24:40.480
Although I can't delve into every detail today, here's a high-level overview of the functioning of this system.
00:25:00.480
The sluggishness of our earlier implementation stems from it constantly rewriting expressions to replace variables, causing their sizes to balloon, which ultimately slows down processing. Landin’s concept centered around maintaining an environment to remember names and values of all variables currently in scope.
00:25:21.760
Instead of rewriting expressions, we retain their original forms while adding binding names and values to the environment as we proceed.
00:25:39.760
So, if we want to evaluate a proc definition being called with an argument, we merely extract the body's definition and create a new environment storing the argument's value during that evaluation.
00:25:57.440
This means we no longer need to rewrite anything; we remember the value of parameter x, enabling us to retrieve its value from the environment when any occurrence arises in the body.
00:26:16.560
To execute this effectively, the machine must be cautious about evaluating definitions since variable bindings in the current environment will be needed later.
00:26:34.560
Landin also invented a data structure called a closure, which couples a definition with its current environment to wrap them together as a singular value.
00:26:55.360
Ultimately, environments and closures are key reasons the SECD machine is more efficient than our expression-rewriting approach.
00:27:11.920
The good news is that we can practically translate the SECD machine’s transition functions into Ruby. This involves direct translations from the definitions in the original paper, with additional cases to evaluate closures and constants properly.
00:27:30.320
While it's certainly feasible to write this more efficiently in Ruby with imperative stack manipulation methods, this version maintains a cleaner correspondence with the foundational concepts of the paper.
00:27:48.960
Here's how the SECD machine performs; it's substantially faster than before, completing tasks in roughly three minutes instead of two hours, marking a fortyfold improvement.
00:28:06.480
Despite this progress, we can enhance performance further.
00:28:23.680
As the SECD machine operates within a loop and contains a switch statement, it's not overly difficult to re-implement it in C, compiling it into native code to achieve additional speed.
00:28:41.120
In C, we can declare a struct for various expressions—variables, calls, definitions, closures, and constants—along with structs for managing the stack, environment, control, and dump.
00:28:58.960
These serve as four distinct types of linked lists for simplicity. Moreover, a more efficient implementation would involve allocating our own contiguous heap to maintain these as a genuine stack.
00:29:16.240
Then, we can translate that destructive version of the evaluating method directly into C, incorporating cases to handle our five types of expressions while facilitating the updates to state during receiver-argument applications.
00:29:34.640
This simplified version doesn't release any allocated memory for environments, closures, or new expressions, meaning a garbage collector would be necessary for real-world scenarios.
00:29:52.920
After compiling the C code as a dynamic library, we can link it to Ruby via the FFI gem. The only requirements are specifying the C data structures and designating which C functions to link as Ruby methods.
00:30:10.560
Some additional helpers are necessary to translate Ruby abstract syntax trees to and from C structs for seamless integration into the evaluation function. Let's skip that for now.
00:30:28.720
Running FizzBuzz with this setup now completes in approximately one minute— three times faster than its Ruby version. While it's not an astronomical improvement since the Ruby variant was already fairly efficient, it is still worthy.
00:30:45.920
As we ponder further optimization possibilities, I won't delve into those intricacies right now, but decades of research have explored ways to enhance the original SECD machine's performance.
00:31:02.720
For instance, during execution, it dynamically translates the original expression into a command list, a process we could opt to perform beforehand, compiling expressions into instructions to expedite execution.
00:31:23.360
Once we generate a command list for the machine, we could translate each one into C or native machine code, eliminating the need for interpretation.
00:31:40.720
If you're interested, follow the link provided at the video's end for more insights into the details of these techniques.
00:31:56.880
What we have explored represents the initial stages of compiling a basic functional language; the extensive research that has taken place since the creation of the SECD machine has unveiled numerous tricks and optimizations for enhancing compiler efficiency.
00:32:12.560
Ten years ago, I concluded "Programming with Nothing" by asking what the purpose of it all is. At that time, I asserted that we had observed an incredibly minimal language possessing the same computational power as Ruby.
00:32:36.480
The only fundamental distinction between that stripped-down language and full Ruby is expressiveness, not capability. The unique charm of Ruby for us comes from how it balances that expressiveness alongside other crucial factors such as performance, safety, and simplicity.
00:32:55.919
In order to answer this same question now, after having previously considered how to code in such a limited language, we’ve seen today how to actually implement that language ourselves.
00:33:10.760
We now possess the fundamental blueprint for constructing and operating our own programming language, equipped with the minimum features required for Turing-complete computation.
00:33:30.080
The earlier talk revealed that this language could write any program; today, we’ve confirmed it can also be engineered in just a few pages of code.
00:33:49.920
From this realization originates a considerable legacy of functional language implementations, many of which are simply optimized or feature-rich versions of what I've just presented.
00:34:05.680
What we've explored represents merely the beginning. A seemingly simple concept like the SECD machine is the first step in an ongoing journey of improvements that ultimately equip us to create languages that are efficient, expressive, and rapid.
00:34:21.760
That's everything I wanted to share with you today. I realize I didn't give you ample opportunity to thoroughly comprehend or read any of the code presented.
00:34:30.080
Everything is available on GitHub if you're interested in taking a look and exploring it to understand how it operates better. I hope you found some of this engaging or entertaining; if not, my apologies.
00:34:49.280
Nonetheless, I genuinely appreciate your time and attention. Thank you very much for watching.