Andy Andrea
Computer science you might (not) want to know
Summarized using AI
Computer science you might (not) want to know
by Andy AndreaIn the presentation titled "Computer Science You Might (Not) Want to Know," Andy Andrea explores the relevance of a Computer Science (CS) degree to the practical work of software developers, particularly in the context of Rails development. He begins by discussing the educational background that typically accompanies a CS degree and notes the dichotomy between academic theory and practical application. Throughout the talk, he evaluates several CS topics through the lens of software development, outlining both their usefulness and applicability. Key points include:
Floating Point Arithmetic: Andrea explains common issues like how floating-point arithmetic can lead to unexpected results, such as 0.1 + 0.2 not equaling 0.3. He elaborates on the binary representation of numbers and discusses the implications of precision when dealing with monetary values. He introduces concepts such as using the Rational class and BigDecimal for better precision in calculations.
Algorithms: The speaker delves into sorting algorithms, using Bubble Sort and Quick Sort as examples to illustrate differences in performance. He explains Big O notation for measuring time complexity and its significance when considering how well code will scale when processing larger datasets.
Real-World Relevance: Andrea emphasizes that knowledge of algorithms is useful not only in coding but also in real-life scenarios, using analogies like searching for a book to explain binary search. He illustrates how algorithm knowledge can enhance problem-solving skills in different contexts beyond programming.
Importance of Scaling and Real-World Metrics: The speaker points out that while understanding algorithmic complexity is important, real-world factors such as database reads/writes or network latency can often become the bigger bottlenecks in software performance.
Practical Learning Approaches: Andrea concludes by reflecting on the paths through which software developers can acquire knowledge, advocating for practical experience gained on the job rather than solely relying on traditional academic routes. He highlights a typical disconnect between academic learning and software development, advocating for a balance between theoretical knowledge and practical skills.
Overall, the session effectively interrogates the relevance of Computer Science education to the everyday realities of software development, particularly for those working with frameworks like Rails, encouraging attendees to consider how they learn and apply technical concepts in their careers.
00:00:12.320
Well, we have 30 minutes, and we have a lot to cover, so let's get started right off the bat.
00:00:20.039
In this talk, we're going to be looking at some topics in computer science through the eyes of software developers and engineers. We will explore how knowing a little bit of computer science can help us when writing code and designing applications, but we'll also discuss why some of these topics might not be particularly relevant to our day-to-day lives.
00:00:33.000
My name is Andy Andrea. I've been working with Rails for about eight years. I graduated with a degree in computer science in 2014, and since then, I've been working at a small consultancy in Durham, North Carolina called Cymed Solutions. We create various types of applications that involve both newer and older versions of Ruby and Rails.
00:00:51.899
I want to clarify that I am a software developer and not an academic or a computer scientist, so this talk comes from that vantage point. Before we dive in, a couple of things to note: when I say 'CS', I mean computer science. If I refer to 'space', we're discussing memory, and if we get into 'logarithms', we will touch on a bit of math, mainly assuming we're working in base two.
00:01:17.820
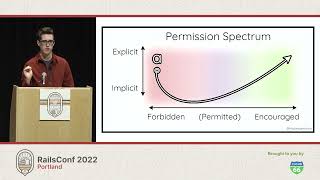
To clarify further, a logarithm is essentially the inverse of an exponent. I can't cover all of computer science in 30 minutes, which is probably for the best, as I exchanged my CS textbooks for a Nintendo Wii U, demonstrating my priorities. Consequently, I've included some magnifying glass emojis on certain slides where you can look up additional topics; those could be things I cut from the talk or related subjects.
00:01:48.240
The first topic we'll discuss today is numbers, specifically starting with everyone's favorite bug: floating-point arithmetic. It's a common issue where you might type a number into a search engine, and it will autocomplete your question. However, I found it quite annoying that neither Google nor DuckDuckGo suggested it as one of the top queries. But if nothing else, I'm pretty sure my talk will be the only one at RailsConf that includes a screenshot of Microsoft Bing.
00:02:12.180
To answer the question of why 0.1 plus 0.2 does not equal 0.3, let's consider how we view numbers. Typically, we think of numbers like 7053, which is equal to that exact value. But by examining each digit, we recognize that the 5 doesn't represent just 'five' — it signifies '50'. The 7 is not merely 'seven' but 'seven thousand'. You can break down the representation of a number into an equation where each digit is multiplied by successive powers of ten.
00:03:21.060
The key aspect here is the base itself. In our typical decimal system, which is base 10, we can use 10 different characters (0-9) to represent a number. When we run out of those characters, we begin adding new digits. However, computers use binary (base 2), which only has two digits: 0 and 1. Therefore, when we transition from base 10, where we progress from '1' to '10' to '11', to binary, we see that '10' in binary is actually '2' in decimal.
00:03:39.060
Continuing with our exploration, we're just looking at computing in binary, comparing it with base 10 over the coming slides. Binary, too, can be broken down into an equation; however, we multiply by powers of 2 instead of powers of 10. For instance, '1111' in binary converts to '15' in decimal, which is distinct from '11' in base 10.
00:04:32.520
We've mostly focused on whole integers, but let's talk about fractional values now. When we look at decimals, the process is similar, only now we're multiplying by negative powers of 10 for values to the right of the decimal point. A quick reminder: a negative exponent means 1 divided by the equivalent positive exponent.
00:05:06.240
Just like we have negative powers in decimal systems, binary fractions use negative powers of 2 to the right of the 'bicimal' point. For example, to represent the decimal value 6.375 in binary, we would need to find the corresponding bits, with 1 in our '2 to the power of -2' and '2 to the power of -3' places. If this information isn't coming together for you, don't worry — this talk isn't just about math; it's more about context.
00:06:11.040
In base 10, many fractional values cannot be expressed in a finite number of digits. For example, 1/3 is generally approximated as 0.33, which is an infinite series repeating the digit 3 after the decimal point. A fascinating point here is that switching bases can allow numbers that typically require infinite space to be represented in a finite format. For instance, 1/3 in base 3 is simply 0.1.
00:06:49.380
Similarly, in base 10, the number 0.2 is easy to understand, but when we try to convert it to base 2, it becomes an infinitely repeating number, represented as 0.0011, which leads to complications with accuracy since we can't perfectly store it in a finite space.
00:07:09.180
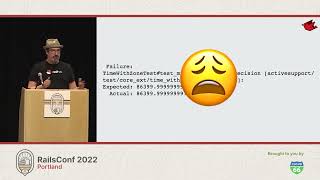
To manage this, we often round or truncate the floating-point numbers we work with in programming languages like Ruby. When looking closely at the actual underlying value of a float in Ruby, you can see that while 0.1, for instance, appears close to 1/10, it is actually slightly larger than that representation. This slight discrepancy leads to the core issue where adding a number slightly larger than 0.1 to a number slightly larger than 0.2 results in a value that is not equal to a number that is slightly smaller than 0.3.
00:07:50.460
Additionally, there are ways to address precision concerns. Instead of creating a decimal for common divisions like 1/3, we can store them as rational equations. Ruby offers us a rational class that allows us to represent values in a precise format. When you check if 1/10 equals 2/20, you can confirm they are identical without losing accuracy when working with rational numbers. However, the downside is that this approach requires more memory.
00:09:03.000
Many developers prefer using BigDecimal rather than float or rational when precision is paramount. BigDecimal offers a good compromise between performance and precision, showing that 0.1 plus 0.2 indeed equals 0.3, but it does come at a memory and performance cost.
00:10:06.620
There are further complications regarding numbers in programming, depending on the language or platform we use. For example, if you're handling large numbers, memory requirements can swiftly escalate. Negative numbers can be represented in ways that might yield unexpected results, like getting a negative total from adding positive values. But in languages like Ruby, we generally don't face as many issues compared to lower-level languages.
00:10:45.659
Understanding how and when to use floats versus decimals is essential; proper handling of financial transactions, for example, is incredibly important. If you use floats for monetary calculations, it can lead to rounding errors that can have profound implications.
00:11:03.000
As Ruby developers, we primarily work with high-level languages, which abstract away many of the low-level mechanics, allowing us to use tools without needing to think about how they operate internally. It’s notable that while technical understanding can be beneficial, we can utilize various programming tools effectively without needing a deep understanding of all the complexities involved.
00:12:22.100
Moving onto the second part, let's talk about algorithms. This topic is more interesting as it involves less math. Algorithms can be considered as processes. If we define them correctly, we can unlock tremendous power in our problem-solving. For example, various algorithms can effectively sort data, with some performing considerably better than others.
00:13:03.000
To illustrate this, let's draw a parallel between sorting algorithms and playing a game of Mario Kart. Much like some players excel, leading the race with speed and efficiency, certain sorting algorithms, like quicksort, perform exceptionally well. Conversely, algorithms like bubble sort may lag behind, similar to a slower racer unable to keep up.
00:14:00.000
Different sorting algorithms excel under different conditions. For instance, depending on the dataset's characteristics—whether it is highly randomized, contains many duplicates, or is nearly sorted—certain algorithms will be more efficient than others. Understanding this versatility allows us to choose the right algorithm for the right situation.
00:15:02.520
Analyzing algorithms involves evaluating their complexity, often expressed through Big O notation, which outlines the worst-case scenario of time complexity. For example, a quicksort has a time complexity of O(n²), indicating that as our input size grows, the execution time will increase significantly.
00:15:55.740
N is representative of the size of our input, which, for sorting algorithms, corresponds to the length of the array we're sorting. If we say that quicksort operates at O(n²), this means that with larger inputs, time complexity will rise substantially, which is not ideal. Instead, we prefer algorithms that increase in complexity at a slower, more manageable rate.
00:16:35.740
Besides O(n) and O(n²), we may encounter other time complexities, each affecting performance in real scenarios. As we examine these calculations more closely, it becomes clear how important it is to consider how code scales with increasing data amounts.
00:17:02.160
Let's explore how we can design an algorithm from scratch. For example, suppose we manage an application that contains an array of books sorted by title. If we want to find a particular book, we might use the Ruby 'find' method to search through the entire list and locate it.
00:17:30.840
In cases where the list isn't lengthy, the 'find' method operates quickly. However, we can optimize this by utilizing the sorted nature of the array. Instead of starting at the beginning, we can jump to the midpoint and compare the current title with the target title. If the current title comes before our target, we can discard the first half of the list, thereby reducing the number of comparisons needed.
00:18:12.480
This method is known as binary search. Ruby has a built-in 'bsearch' method that efficiently locates a target value by employing this logic. If the data is sorted, we can quickly zero in on the desired item while minimizing unnecessary operations.
00:19:02.640
As we discuss binary search, it's essential to note that if our dataset is not sorted, our assumptions break down. Additionally, the order of operations in our comparison can be critical, as Ruby relies on operators that are sensitive to input order.
00:19:35.520
The binary search technique also has practical applications beyond programming. Tools like 'git bisect' utilize a similar principle of binary search to locate specific commits that introduce bugs or other issues. This highlights how critical understanding algorithms is, as they often require human input to confirm outcomes.
00:20:20.640
Recognizing algorithms as a broader concept can enhance our problem-solving abilities. For instance, when looking for a specific book in a library, we don't inspect every title but rather navigate through sections to locate it.
00:21:19.320
Understanding algorithms enables us to leverage them effectively in our coding practices, whether that means implementing our own or utilizing existing methods like Ruby's 'bsearch'. Moreover, we can analyze data structures using similar complexity metrics, offering insights into time and resource efficiency.
00:22:30.780
Algorithmic complexity gives us a framework for considering how our code will scale as data continues to grow. This is particularly timely, given how the volume of data is expanding exponentially. Being able to communicate effectively about these complexities with our colleagues is vital. For instance, suggesting a binary search algorithm is more efficient than simply expressing it as a generalized concept.
00:23:50.760
However, it is crucial to recognize that algorithmic complexity may not always be the primary bottleneck in our applications. For example, database interactions, file access, and network communications take significant time and resources, sometimes outweighing any algorithmic concerns.
00:25:16.440
Additionally, algorithmic complexity can be misleading as a primary measure of efficiency because it glosses over practical, real-world factors like constants and coefficients that also affect performance. For example, a seemingly more efficient O(n) algorithm might be outperformed by an O(n²) algorithm for specific data sizes, simply based on the environmental conditions in which they operate.
00:26:28.740
We should utilize benchmarking and profiling methods to gain realistic insights into performance. The tools we use often come optimized for us, meaning that handheld implementations can fall short of built-in solutions. The advantages offered by high-level languages like Ruby should not be underestimated; they abstract away many complexities that would otherwise burden us.
00:27:29.400
At this point, let’s reflect on why computer science matters. A significant aspect involves preparing for job interviews where technical knowledge is commonly tested. Understanding foundational theory and engaging with advanced topics can provide value and context, though it's worth noting that software development and computer science are increasingly more disparate fields.
00:28:29.760
Even if one does not have a formal computer science background, practical experience, such as through boot camps, often equips developers with the skills necessary for success without delving into academic theory excessively. The key takeaway is that many programming concepts in computer science can be acquired on the job. If you encounter discrepancies in floating-point arithmetic, for instance, you are likely to seek solutions through online resources instead of a lengthy classroom lecture.
00:29:46.860
In conclusion, you can learn about computer science in various ways, whether through self-study, mentorship, or attending talks. A heartfelt thank you to all my co-workers and mentors, especially Carrie Miller for her advice and Billy Frye for helping me trim this talk down to size.
Explore all talks recorded at RailsConf 2022
+64